[프로그래머스] 정수 삼각형(C++)

문제 설명

위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다.

아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다.

예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.

삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.

 

제한 사항

• 삼각형의 높이는 1 이상 500 이하입니다.
• 삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.

 

 

입출력 예

triangle	result
[[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]]	30

 

 

Solution

2차원 배열이 입력되면 그 형태는 아래와 같다.

 

dp[i][j] = (i, j)까지의 최대합 이라고 정의하면

dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]) + triangle[i][j]

점화식은 위와 같다.

단, i == 0인 경우(제일 왼쪽 줄)와 j == i 인 경우(제일 오른쪽 줄)만 예외처리 해주면 끝~!

 

dp 배열을 모두 채운 후의 형태는 아래와 같다.

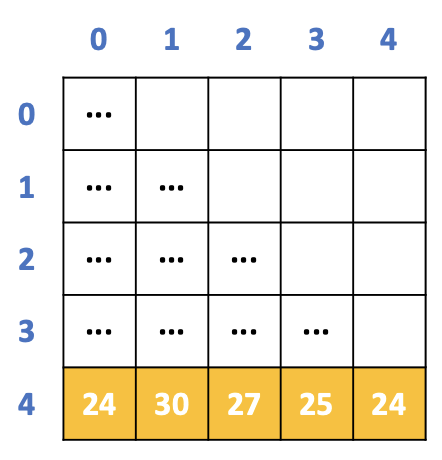
보통 dp 문제의 답은 제일 마지막 칸의 값인데

이 문제는 제일 마지막 줄 중 가장 큰 값을 또 찾아서 정답으로 출력해야 한다!

따라서 정답은 30~!

 

 

Answer(C++)

// [프로그래머스] 정수 삼각형
// https://programmers.co.kr/learn/courses/30/lessons/43105
// dp

#include <string>
#include <vector>

using namespace std;

int solution(vector<vector<int>> triangle) {
    int length = triangle.size() - 1;
    int answer = 0;
    int dp[501][501];
    dp[0][0] = triangle[0][0];
    
    for(int i = 1 ; i <= length ; i++) {
        for(int j = 0 ; j <= i ; j++) {
            if(j == 0) { // 제일 왼쪽 줄
                dp[i][j] = dp[i-1][j];
            }
            else if(j == i) { // 제일 오른쪽 줄
                dp[i][j] = dp[i-1][j-1];
            }
            else {
                dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]);
            }
            dp[i][j] += triangle[i][j];
        }
    }
    
    // dp 배열의 제일 마지막 줄 중 가장 큰 값
    answer = dp[length][0];
    for(int i = 1 ; i <= length ; i++) {
        if(dp[length][i] > answer) {
            answer = dp[length][i];
        }
    }
    
    return answer;
}