Red-Black Tree

레드 블랙 트리는 균형 이진 탐색 트리로 탐색, 삽입, 삭제 모두 시간 복잡도가 logN이다.
각 노드는 빨간색 또는 검은색의 색상을 나타내는 추가 비트를 저장하고, 추가된 비트는 삽입 또는 삭제의 과정에서 트리가 균형을 유지하도록 하는 데 사용된다.
대표적으로 C++ STL의 set, multiset, map, multimap 이 레드 블랙 트리를 이용하여 구현되어있다.
Why Red-Black Tree?
왜 레드 블랙 트리를 사용하는 걸까?
이 이유에 대해 알기 위해서는 BST(이진 탐색 트리)의 단점부터 파악해야 한다.
BST란, 노드의 오른쪽 하위 트리에는 노드 값보다 큰 값이 있는 노드만 포함되고, 왼쪽 하위 트리에는 노드 값보다 작은 값이 들어 있는 트리를 말한다.
따라서 BST는 검색하기에 용이한 구조이고 평균적으로 O(logN)의 시간 복잡도를 가진다.
하지만 최악의 경우(예를 들어 1 → 2 → 3 → 4 순서로 삽입하는 경우) 트리가 선형적이 되고 이때의 시간 복잡도는 O(N)이다.
이처럼 BST는 삽입 순서에 따라 트리의 형태가 선형적으로 변할 수 있기에 탐색에 있어 항상 O(logN)라는 것을 보장해주지 못한다.
항상 높이가 logN임이 보장된다면 최악의 경우에도 O(logn)의 상한을 보장할 수 있고, 레드 블랙 트리는 추가 비트를 통해 높이를 항상 logN으로 보장해주기에 이것을 사용하는 것이다.
Red-Black Tree 규칙
1. 모든 노드는 빨간색 또는 검은색이다.
2. 루트 노드는 항상 검은색이다.
3. 빨간색 노드끼리는 인접할 수 없다.(빨간색 노드는 빨간색 부모 또는 빨간색 자식 노드를 가질 수 X)
4. 노드(루트 포함)에서 하위 NULL 노드까지의 모든 경로는 동일한 수의 검은색 노드를 가진다.
5. 모든 리프 노드는 검은색 노드이다.
Red-Black Tree 특징
레드 블릭 트리가 위의 5가지 규칙을 모두 만족하게 되면 중요한 특징이 하나 생긴다.
(루트 노드 ~ 가장 먼 리프 노드)까지의 거리가 (루트 노드 ~ 가장 가까운 리프 노드)까지의 거리의 두 배 보다 항상 작다는 것.
수학적으로 생각해봐도 우선 레드 블릭 트리는 균형 BST이기 때문에 왼쪽과 오른쪽 노드의 높이 차가 1 이하이다.
규칙 2와 5에 따라 루트와 리프 노드는 무조건 검은색이고, 규칙 4에 따라 모든 경로에서의 검은색 노드 수는 동일하다.
예를 들어 depth가 3인 경로에서도, depth가 4인 경로에서도 검은색 노드의 수는 3개이기 때문에 4 < 3 * 2가 성립한다.
(루트 노드 ~ 가장 먼 리프 노드) < (루트 노드 ~ 가장 가까운 리프 노드) * 2다시 말해서 레드-블랙 트리는 대략적으로으로 균형이 잡힌 상태가 된다. 따라서, 삽입, 삭제, 검색 시 최악의 경우에서의 시간 복잡도가 트리의 높이에 따라 결정되기 때문에 BST에 비해 효율적이라고 할 수 있다.
Red-Black Tree의 탐색 연산
레드 블랙 트리는 이진트리의 특별한 경우이기 때문에 레드 블랙 트리의 탐색 알고리즘은 이진트리의 탐색 알고리즘과 유사하다.
루트 노드부터 탐색하면서 아래의 과정을 반복하면 된다.
1. 현재 노드 = 찾는 값 -> return;
2. 현재 노드 < 찾는 값 -> 오른쪽 subtree;
3. 현재 노드 > 찾는 값 -> 왼쪽 subtree;
Red-Black Tree의 삽입 연산
레드 블릭 트리는 균형 이진 탐색 트리이기 때문에 일단 BST의 원칙에 따라 새로운 원소를 삽입하고 이 노드를 빨간색으로 지정한다.
만약 검은색으로 지정한다면 규칙 4를 위반할 위험이 있기 때문에 새로운 노드는 무조건 빨간색으로 지정하는 것!
규칙 4를 준수하기 위해 새로운 노드를 빨간색으로 만들긴 했지만, 이러면 빨간색 노드끼리 인접하는 경우(Double Red)가 발생하기 때문에 규칙 3을 위반할 수 있다.
이때 아래의 두 가지 방법을 사용하여 재구조화하는 작업이 필요하다.
1. Recoloring
2. Rotation
1) Recoloring

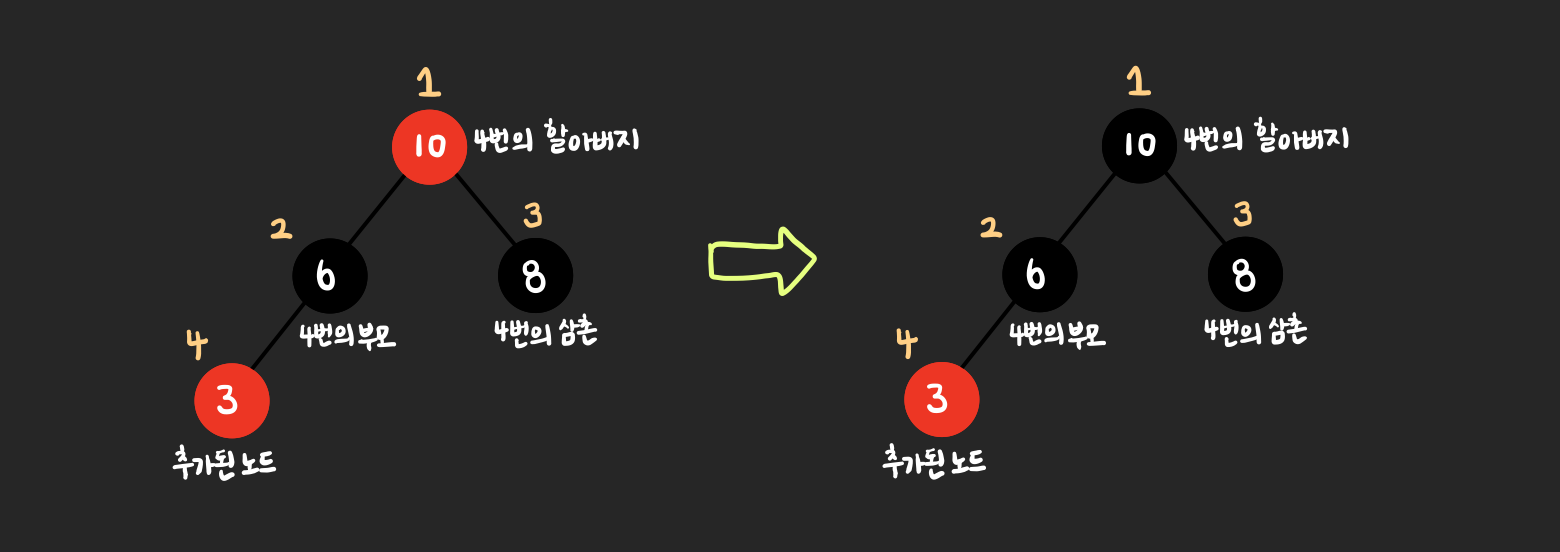
Recoloring은 위의 그림과 같이 삽입된 노드의 삼촌 노드 즉, 내 부모의 형제 노드의 색상이 빨간색일 때 발생한다.
먼저 새로운 노드를 BST에서와 같이 추가하고 노드(4번)가 루트 노드이면 검은색으로 변경, 그렇지 않으면 상위 노드(2번)의 색상을 확인한다.
만약 상위 노드(2번)의 색상이 검은색이면 변경하지 말고 빨간색이라면 노드의 삼촌(3번) 색상을 확인해야 한다.
노드의 삼촌이 빨간색인 경우, 노드의 부모와 삼촌의 색상은 검은색으로, 할아버지의 색상은 빨간색으로 변경한다.
이때 할아버지 노드가 루트 노드라면 검은색으로 변경한 후 종료하고, 만약 할아버지의 아버지 노드가 빨간색이라면 빨간색 노드끼리는 인접할 수 없다는 3번 규칙을 위반하므로 할아버지에 대해 동일한 과정을 반복해야 한다.
// Recoloring 수도 코드
if(루트 노드)
1번 규칙에 따라 검은색으로 색상 변경 // 1번 규칙: 루트 노드 = 검은색
else {
// 상위 노드 색상 check
if(상위 노드 == black) 변경 X
else { // 상위 노드 == red
if(삼촌 노드 == red) {
부노 노드 = black
삼촌 노드 = black
할아버지 노드 = red
if(할아버지 노드 == 루트 노드)
종료
else
할아버지 노드에 대해 동일한 과정 반복
}
}
}
2) Rotation

Rotation은 Recoloring과 반대로 새로운 노드의 삼촌 노드가 검은색일 때 수행한다.
Rotation은 다시 크게 2가지 경우로 나눌 수 있다.
1. Left Rotate
2. Right Rotate
1️⃣ Left Rotate
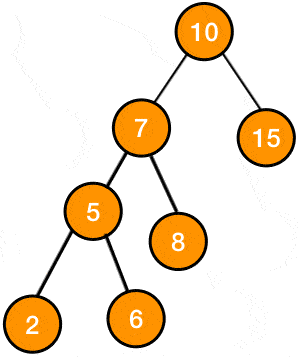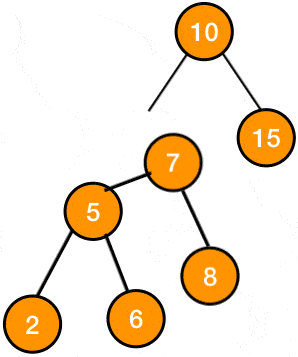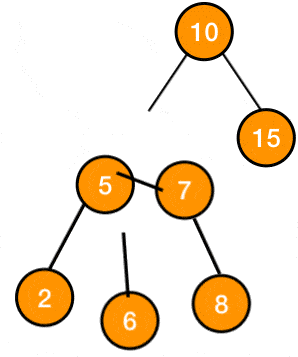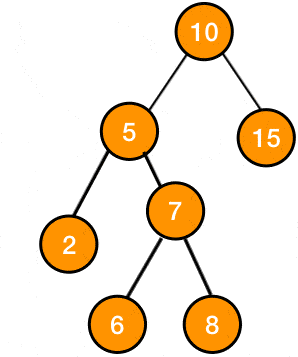
Left Rotate는 현재 노드와 왼쪽 자식 노드의 위치를 바꾸는 것이다.
RBT는 BST이기 때문에 이 둘의 위치를 맘대로 바꾸면 왼쪽 자식은 루트 노드보다 작아야 한다는 BST의 원칙을 위반하게 된다.
따라서 이들이 포함된 subtree 전체를 회전시켜줘야 한다. 아래의 움직이는 이미지를 보면 무슨 소린지 감이 올 것이다.

2️⃣ Right Rotation
Right Rotation은 left rotation과 반대이다. 현재 노드와 오른쪽 자식 노드를 swap 하고, BST의 원칙을 준수할 수 있게 나머지 노드들도 조정해주면 된다.
Red-Black Tree의 삭제 연산
삭제도 삽입과 마찬가지로 BST의 특성을 유지하면서 해당 노드를 삭제한다. RBT의 삽입 연산에서는 삼촌의 색상을 확인해서 Recoloring을 할 것인지, Rotation을 할 것인지 결정했다.
삭제 연산에서는 삼촌이 아닌 형제의 색상을 확인하여 적절한 경우를 결정한다.
삭제해야 할 노드를 찾아서 삭제하고 나면 규칙 3(Double Red)이 위반될 우려가 있다.
(삭제한 노드의 부모와 자식이 모두 빨간색인 경우)
또한, 삭제할 노드가 검은색 노드라면 규칙 4 즉, 모든 경로에서의 검은색 노드의 수가 달라질 우려가 있다. 따라서 삭제는 삽입보다 좀 더 복잡한 과정이다.
삽입 과정에서는 두 개의 빨간색 노드가 인접하는 Double Red가 발생했지만, 삭제 과정에서는 두 개의 검은색 노드가 인접하는 Double Black이 발생할 수 있다. 우리가 해야 할 것은 이 Double Black을 Single Black으로 변환하는 것이다.
삭제 연산의 자세한 과정에 대해 정말 자세히 설명해둔 글이 있어서 자세한 내용은 아래 글을 참고하면 좋을 것 같다.
레드블랙트리 - 삭제
레드블랙트리 삭제 레드블랙트리의 삭제는 기본적으로 이진탐색트리의 삭제에 기반 한다. 이렇게 노드를 삭제하고 나면, 무너진 레드블랙트리의 규칙을 복원하는 것에 초점을 둔다. 첫째로 삭
assortrock.com
References
Interview_Question_for_Beginner/tree/master/DataStructure#red-black-tree
'CS > 자료구조' 카테고리의 다른 글
| 그래프 (0) | 2022.10.08 |
|---|---|
| Hash Table (0) | 2022.09.30 |
| Heap(Max Heap, Min Heap) (0) | 2022.09.29 |
| Tree(Binary Tree, 포화 이진 트리, 완전 이진 트리, BST) (0) | 2022.09.25 |
| Stack & Queue (0) | 2022.09.25 |
